Prediction of the Toroidal form of Black Hole
I was right regarding my prediction of the Toroidal form of Black Hole. Toroidal topology is possible in string theory, even in classical GR similar ring type of event horizon exist for rotating BH. And most important thing is that Toroidal Black Hole is helpful in explaining the structure of Quasar and other AGN, Active Galactic Nuclei. Here is a short note on my work. Very soon I will try to do some calculations.
A black hole is a fascinating topic nowadays. As we know that Einstein theory of Gravity gives the dramatic prediction that sufficiently dense star collapses to form a black hole. In scientific language, it is spacetime singularity surrounded by the horizon. An observer can enter inside the horizon but he can not return back beyond the horizon. A black hole has a mass, they can carry a charge and angular momentum means they can rotate. But except these, they don’t have any other classical characteristics.
I am interested here in the shape of a black hole. Is there a well-defined shape of the black hole? Or horizon of a black hole can take any shape? First, we should think that after all BH is an Astrophysical object and every Astrophysical object should satisfy certain conditions to be stable. Then we will think what is the maximum possibility regarding the shape of BH. So what are the conditions for the stability of an astrophysical object? These conditions are defined as energy conditions in General relativity.
These conditions are:
1. Null Energy Condition.
2. Weak Energy Condition,
3. Dominant Energy Condition.
4. Strong Energy Condition.
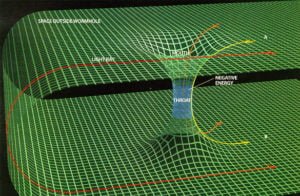
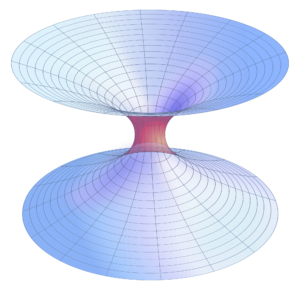

First I should introduce you one quantity known as energy-momentum tensor, which describes the distribution of mass, momentum, and stress due to matter.
Technically every condition defines a certain type of density and pressure condition for the perfect fluid matter. These conditions are important in General relativity to prove No Hair theorem in BH and entropy of BH. Let us assume BH has a shape other than spheroid or ellipsoid. Then what is the possibility of the existence of BH? Let us consider a Toroid shape BH means event horizon of BH is in a toroid shape. This condition of BH is very well discussed in the case of Kerr’s BH.
When a heavy massive spherical rotating body collapse under its own gravity. Its distribution of mass no longer remains spherical and equatorial bulge. Because point can not support a rotation in classical physics, so the minimum shape of singularity is a ring with zero thickness and non-zero radii. It is sometimes known as Kerr’s Singularity.
An observer falling into this type of black hole may be able to avoid the central singularity. This type of BH sometimes behaves like a wormhole. But BH shape can not be toroid shape just due to No hair Theorem. Because toroidal shape can generate noticeable ‘hairs’ that the outside observers could feel. When I am talking here the shape of BH. I mean topology of BH. In classical GR there is no chance of toroidal BH. But in higher dimensional theory like String theory, we can discuss toroidal BH. This type of black hole is important to explain the structure of Quasars and other active galactic nuclei.

http://scienceteen.com/a-black-hole-of-gargantuan-proportion-at-the-centre-of-galaxies/