The golden ratio
The Mathematics of Nature and Aesthetics

The golden ratio is an irrational number approximately equal to 1.61803 and is sometimes denoted by φ(Phi) after the mathematician Phidias who studied its properties. Its unique properties were first considered in the idea of dividing a line into two segments such that the ratio of the total length to the length of the longer segment is equal to the ratio of the length of the longer segment to the length of the shorter segment.
Who was Fibonacci?

Fibonacci Leonardo Pisano also known as Leonardo Pisano or Leonard of Pisa, was born in Pisa, Italy in 1175 AD. He Grew up with a North African education under the Moors and received his early education from a Muslim schoolmaster. He traveled around the Mediterranean coast and met with many merchants and learned their systems of arithmetic. He realized the advantages of the Hindu-Arabic system and was one of the first to introduce the Hindu-Arabic number system to Europe- the system used today. He was the most outstanding mathematician of the European Middle Ages.Little is know about his life except for the few facts given in his mathematical writings. His first book was published in 1202 called Liber Abaci. This book is devoted to arithmetic and elementary algebra.
His next book, Practica Geometriae, he wrote in 1220, presents geometry and trigonometry with Euclidean origin.He applied algebra to solve geometric problems and geometry to solve algebraic problems. This was uncommon in Europe at the time. He also wrote two other books. One of which included Liber Quadratorum which earned him the reputation as a major number theorist. Liber Abaci remained the European standard for more than two centuries replacing the Roman numeration system. In his honor, a statue of Fibonacci stands in a garden across the Arno River, near the Leaning Tower of Pisa.
The Fibonacci Number

Were introduced in The Book of Calculating.The Series begins with 0 and 1. Next number is found by adding the last two numbers together. The number obtained is the next number in the series. The Pattern is repeated over and over
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …
as we continue the sequence, the ratios seem to be converging upon one number (from both sides of the number)!
2/1 = 2.0 (bigger)
3/2 = 1.5 (smaller)
5/3 = 1.67(bigger)
8/5 = 1.6(smaller)
13/8 = 1.625 (bigger)
21/13 = 1.615 (smaller)
34/21 = 1.619 (bigger)
55/34 = 1.618(smaller)
89/55 = 1.618
Here the ratios are rounded off to the third decimal place. If we examine 55/34 and 89/55 more closely, we see that their decimal values are not the same. But as the numbers in the sequence get larger and larger the ratio will eventually become the same number, and that number is called the Golden Ratio!

The Mona Lisa

Measure the length and the width of the painting itself. The ratio is, of course, Golden. Draw a rectangle around Mona’s face (from the top of the forehead to the base of the chin, and from left cheek to right cheek) and notice that this, too, is a Golden rectangle.
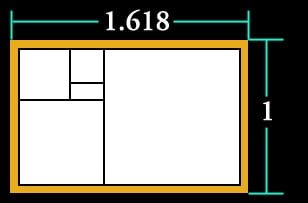
The golden rectangle


The golden rectangle can be constructed from these line segments so that the length to width ratio is φ. The golden rectangle may be divided into a square and a smaller golden rectangle. The ancient Greeks believed that a rectangle constructed in this manner was the most aesthetically pleasing of all rectangles and they incorporated this shape into a lot of their art and architectural designs. What does this have to do with fibonacci numbers?
Constructing A Golden Rectangle
It’s strange that the Golden Ratio comes in such unexpected places? Let’s see if we can find out why. The Greeks were the first to call phi the Golden Ratio and associated the number with perfection. It seems to be part of human nature or instinct to find things that contain the Golden Ratio naturally attractive – such as the “perfect” rectangle. Realizing this, designers have tried to incorporate the Golden Ratio into their designs so as to make them more aesthetically apealing to the eye. Doors, notebook paper, textbooks, etc. all seem more attractive if their sides have a ratio close to phi. Now, let’s construct our own “perfect” rectangle
Method One
Make any square and bisect it. Draw a diagonal of one of the rectangles and measure the length of the diagonal and make a note o;”>1
1
2
3 1.5000000000000000
5 1.6666666666666700
8 1.6000000000000000
13 1.6250000000000000
21 1.6153846153846200
34 1.6190476190476200
55 1.6176470588235300
89 1.6181818181818200
144 1.6179775280898900
233 1.6180555555555600
377 1.6180257510729600
610 1.6180371352785100
987 1.6180327868852500
1,597 1.6180344478216800
2,584 1.6180338134001300
4,181 1.6180340557275500
6,765 1.6180339631667100
10,946 1.6180339985218000
17,711 1.6180339850173600
28,657 1.6180339901756000
46,368 1.6180339882053200
75,025 1.6180339889579000
The Golden Ratio is an irrational number with an infinite number of decimal places and it never repeats itself! Generally, we round the Golden Ratio to 1.618.
The Golden Ratio is not just some number that mathematicians think is cool. The interesting thing is that it comes in strange places that we may not ordinarily think. Fibonacci did not “invent” the Golden Ratio, he just discovered one instance of where it appeared naturally. In fact, civilizations such as the Ancient Egyptians, the Mayans, as well as the Greeks discovered the Golden Ratio and incorporated it into their own art, architecture, and designs. They discovered that the Golden Ratio seems to be Nature’s perfect number. For some reason, it just seems to appeal to our natural instincts and fits in our aesthetical fantasies. The most basic example is in rectangular objects.



Now observe, which of them seem to be the most naturally attractive rectangle? If you think the first one, then you are probably the type of person who likes everything to be symmetrical. Most people tend to think that the third rectangle is the most appealing. The length to width ratio for each rectangle is:
Rectangle I: Ratio 1:1
Rectangle II: Ratio 2:1
Rectangle III: Ratio 1.618:1
The third rectangle is the most appealing because the ratio is the Golden Ratio! For centuries, designers of art and architecture have recognized the significance of the Golden Ratio in their work.
Golden ration In music
Lets take a look at the piano keyboard…do you see anything familiar?
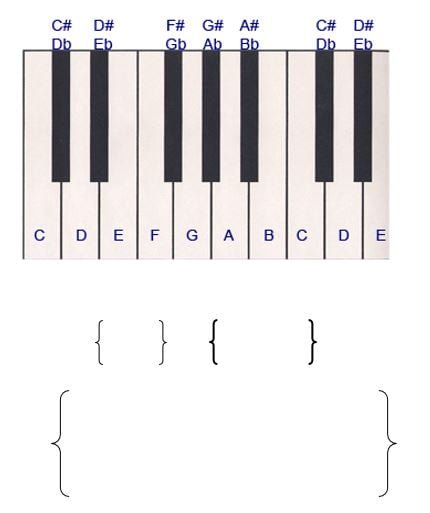
Count the number of keys (notes) in each of the brackets and You will see the numbers 2,3,5,8,13….coincidence? It looks like the Fibonacci sequence because it is! Music involves several applications of Fibonacci numbers. A full octave is composed of 13 total musical tones, 8 of which make up the actual musical octave
The ancient temples fits almost precisely into a golden rectangle. Further classic subdivisions of the rectangle align perfectly with major architectural features of the structure.



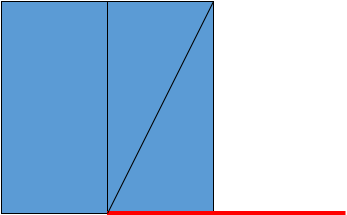
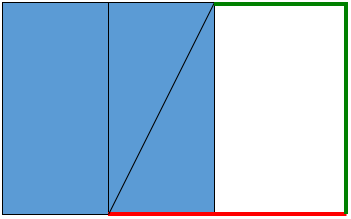
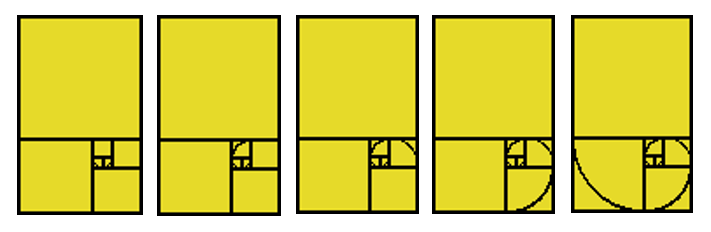
Method Two
Make a square (small to conserve space), Please note that the golden area is what the rectangle will eventually look like. Now, build another, congruent square right next to the first one. Now we have a rectangle with a width 1 and length 2 units and build a square on top of this rectangle such that square formed will have a side of 2 units. Now we have a new rectangle with width 2 and length 3.
Let’s continue the process, building another square on the right of our rectangle. This square will have a side of 3. Now we have a rectangle of width 3 and length 5. Again, let’s build upon this rectangle and construct a square underneath, with a side of 5. The new rectangle has a width of 5 and a length of 8. Let’s continue to the left with a square with side 8. Have you noticed the pattern yet? The new rectangle has a width of 8 and a length of 13.
Let’s make one final square on top, with a side of 13. Our final rectangle has a width of 13 and a length of 21. Notice that the constructed golden rectangle using a square have side lengths from the Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, …)! No wonder our rectangle is golden! Each successive rectangle has a width and length same as consecutive terms in the Fibonacci sequence. If we divide the length by the width, we get the Golden Ratio! Of course, our rectangle is not “perfectly” golden but if we keep on going the ratio becomes better, for our purpose a length of 21 and a width of 13 are sufficient. This rectangle should seem very well proportioned to you, i.e. it should be pleasing to the eye. If it isn’t, maybe you need your eyes checked!







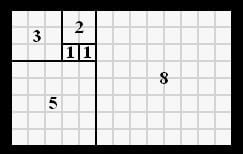
If the two smallest squares have a width and height of 1, then the box to their left has a measurement of 2 and the other boxes measure 3, 5, 8, and 13.

Constructing a Golden Spiral
The golden ratio is expressed in spiraling shells. There is a quarter of a circle in each square going from one corner to the opposite. This is not a true mathematical spiral. We built our rectangle in a counterclockwise direction which leads us into another interesting aspect of the Golden Ratio. Look at the rectangle with all of our construction lines drawn in and concentrate on the squares that we drew, starting with the two smallest ones. Let’s start with the one on the right. Connect the upper right corner to the lower left corner with an arc that is 1/4th of a circle.
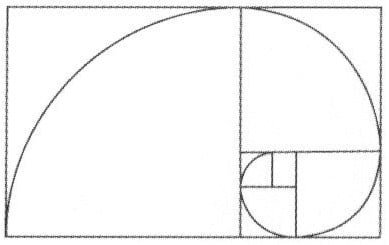

Then draw an arc that is one-fourth of a circle into the second square on the left, We will continue this process until each square has an arc inside of it, with all of them connected as a continuous line. The line should look like a spiral. Here is an example of what your spiral should look like:
Fibonacci numbers in nature

Look at any seed head, it looks like spiral patterns curving out from the center-left and right. If you count these spirals to the left and then the right you will notice that these are two consecutive Fibonacci numbers. This can also be seen in pinecones, pineapples, cauliflower, and many more!
More Fibonacci numbers in nature

Most of the time, the number of petals on a flower is a Fibonacci number! This means that this “golden spiral” occurs frequently in nature. If you look closely enough, you might find a golden spiral in the head of a daisy, in a pinecone, in sunflowers, or in a nautilus shell that you might find on a beach or even in your ear! Here are some examples:




Some Flower Petal Examples
3 petals: lilies
5 petals: buttercups, roses
8 petals: delphinium
13 petals: marigolds
21 petals: black-eyed susans
34 petals: pyrethrum
55/89 petals: daisies
Leaves and Branching Plants
Leaves are also found in groups of Fibonacci numbers.Branching plants always branch off into groups of Fibonacci numbers.Think about yourself, You should have:
5 fingers on each hand
5 toes on each foot
2 arms
2 legs
2 eyes
2 ears
2 sections per leg
2 sections per arm
I could go on, but I think you get the point.
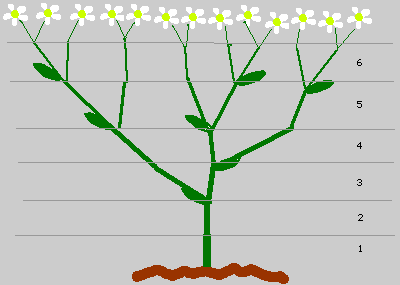
So, why do the shapes that exhibit the Golden Ratio seem to be more appealing to the human eye? No one fully understands this. But we have evidence that the Golden Ratio seems to be Nature’s perfect number. It’s easily discoverable that the florets of the daisy (and of a sunflower as well) grow in two spirals extending out from the center.
The first spiral has 21 arms, while the other has 34. Do these numbers sound familiar? They should – they are Fibonacci numbers! And their ratio, of course, is the Golden Ratio. The same applies to pinecone, where spirals from the center have 5 and 8 arms, respectively (or of 8 and 13, depending on the size)- again we have two Fibonacci numbers:


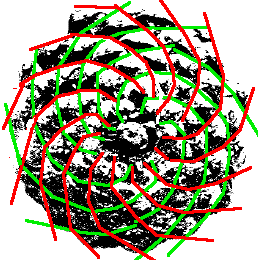
A pineapple has three arms of 5, 8, and 13 – even more evidence that this is not a coincidence. Is Nature playing some kind of game with us? No one knows for sure, but scientists speculate that plants that grow in spiral formation do so in Fibonacci numbers because this arrangement makes for the perfect spacing for growth and provide the perfect arrangement for maximum growth potential and survival of the plant.
The Human Body


Do these faces seem attractive to you? Many people seem to think so. But why? Is there something specific in each of their faces that makes them attractive, or is our sense of attraction is governed by Nature’s rules? Does this have anything to do with the Golden Ratio?
I think you already know the answer to that question. Let’s analyze these faces and see if the Golden Ratio is present or not. Here’s how we are going to conduct our search for the Golden Ratio. We will measure certain aspects of each person’s face. Then we will compare their ratios. Let’s begin. We will need the following measurements, to the nearest tenth of a centimeter.

a = Top-of-head to chin
b = Top-of-head to pupil
c = Pupil to nosetip
d = Pupil to lip
e = Width of nose
f = Outside distance between eyes
g = Width of head
h = Hairline to pupil
i = Nosetip to chin
j = Lips to chin
k = Length of lips
l = Nosetip to lips
Now find the following ratios:
a/g , b/d , i/j , i/c, e/l, f/h, k/e .
The blue line defines a perfect square of the pupils and outside corners of the mouth. The golden section of these four blue lines defines the nose, the tip of the nose, the inside of the nostrils, the two rises of the upper lip and the inner points of the ear. The blue line also defines the distance from the upper lip to the bottom of the chin.
The yellow line, a golden section of the blue line, defines the width of the nose, the distance between the eyes and eye brows and the distance from the pupils to the tip of the nose.The green line, a golden section of the yellow line defines the width of the eye, the distance at the pupil from the eye lash to the eye brow and the distance between the nostrils. The magenta line, a golden section of the green line, defines the distance from the upper lip to the bottom of the nose and several dimensions.

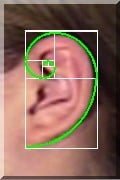

Even when viewed from the side, the human head illustrates the Divine Proportion. The first golden section (blue) from the front of the head defines the position of the ear opening. The successive golden sections define the neck (yellow), the back of the eye (green) and the front of the eye, and the back of the nose and mouth (magenta). The dimensions of the face from top to bottom also exhibit the Divine Proportion, in the positions of the eyebrow (blue), nose (yellow), and mouth (green and magenta). The ear reflects the shape of a Fibonacci spiral.
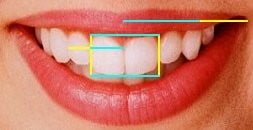
The front two incisor teeth form a golden rectangle, with a phi ratio in the height to the width.The ratio of the width of the first tooth to the second tooth from the center is also phi.The ratio of the width of the smile to the third tooth from the center is phi as well. Visit the site of Dr. Eddy Levin for more on the Golden Section and Dentistry.
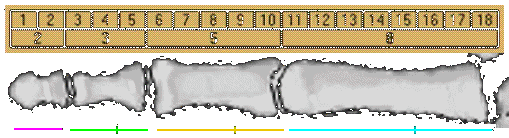

The ratio of your forearm to hand is Phi


The human body is based on Phi and illustrates the Golden Section.
White line: body’s height.
Blue line:
a golden section of the white line, defines the distance from the head to the finger tips.
Yellow line:
a golden section of the blue line, defines the distance from the head to the navel and the elbows.
Green line:
a golden section of the yellow line, defines the distance from the head to the pectorals and inside top of the arms, the width of the shoulders, the length of the forearm and the shin bone.
Magenta line:
a golden section of the green line, defines the distance from the head to the base of the skull and the width of the abdomen. The sectioned portions of the magenta line determine the position of the nose and the hairline.
Although not shown, the golden section of the magenta line (also the short section of the green line) defines the width of the head and half the width of the chest and the hips.
The Fibonacci Sequence
The sequence in which each number is the sum of the two preceding numbers.This sequence is defined by the linear recurrence equation.
Fn = Fn-1 + Fn-2
F 1 = F2 = 1
F 2 = 1
By the above definition the Fibonacci numbers for n=1, 2 is 1 and the sequence continues as:
1, 1, 2, 3, 5, 8, 13, 21,…
Before Fibonacci, these numbers were already investigated by Indian Scholars in rhythmic patterns of syllables. The ratio of successive Fibonacci numbers is something you might be surprised by! As n increases, the ratio of Fn / Fn-1 approaches the golden ratio and is expressed as

which is equal to

This is the fundamental property of both the Fibonacci sequence and the golden ratio. Both of these ratios converge at the same limit which is the positive root of the quadratic equation
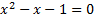
Fibonacci’s rabbits
In Fibonacci’s book Liber Abcai there is a question involving the reproduction of a pair of rabbits.Suppose a newly born pair of rabbits (a male and female) are put in a field. The rabbits are able to mate at the age of one month so that at the end of the second month a female can produce another pair of rabbits. Assuming that the rabbits never die and the female always produces a new pair every month from the second month on. How many pairs will there be in one year?
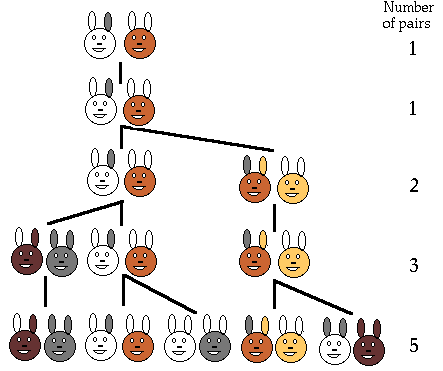
Answer: 144 rabbit
References
1. The Golden Ratio and Fibonacci
Numbers, by Dunlap Richard A
2. www.goldennumber.net
3. http://goldenmeangauge.co.uk
Written by: Prashant Kumar Sinha